добавления.рф -
купить или арендовать доменное имя онлайн- Домены с синонимами добавления
- Покупка
- Аренда
- Добавления.рф
- 70 000
- 700
- Домены начинающиеся с добавлени
- Покупка
- Аренда
- добавление.рф
- 100 000
- 1 000
- Домены с синонимами, содержащими добавлени
- Покупка
- Аренда
- prilezhanie.ru
- 50 000
- 500
- prilozhenia.ru
- 50 000
- 500
- prilozheniya.ru
- 200 000
- 2 000
- uvelichenie.ru
- 50 000
- 500
- uvlechenija.ru
- 50 000
- 500
- uvlecheniya.ru
- 50 000
- 500
- Добавочка.рф
- 70 000
- 700
- Добавочки.рф
- 70 000
- 700
- дополнения.рф
- 88 000
- 880
- Пополнение.рф
- 100 000
- 1 000
- пополнения.рф
- 88 000
- 880
- Прилежание.рф
- 70 000
- 700
- приложение.рф
- 800 000
- 8 000
- приложений.рф
- 60 000
- 600
- приложения.рф
- 100 000
- 1 000
- увеличение.рф
- 100 000
- 1 000
- увлеченье.рф
- 70 000
- 700
- увлеченья.рф
- 70 000
- 700
- химдобавки.рф
- 100 000
- 1 000
- Домены с переводом, содержащими добавлени
- Покупка
- Аренда
- addition.ru
- 50 000
- 500
- appendiks.ru
- 50 000
- 500
- preservatives.ru
- 100 000
- 1 000
- Аддон.рф
- 100 000
- 1 000
- презерватив.рф
- 500 000
- 5 000
- Аренда или покупка домена шлифмашины.рф: Преимущества и стратегии продвижения
- Изучите преимущества обладания доменным именем шлифмашины.рф для повышения узнаваемости бренда и укрепления имиджа в отрасли.
- Шедеврики.рф: Почему Вам стоит купить или арендовать это доменное имя
- Оптимизируйте свою онлайн-присутствие с шедеврыки.рф – уникальным и запоминающимся доменным именем, обеспечивающим креативность, запоминаемость и расширенную возможность продвижения в российском сегменте интернета.
- Доменное имя эйчар.рф - Рецепт успеха для бизнеса и онлайн-позиционирования
- Доменное имя эйчар.рф - это не только доступ к обширной аудитории, но и ключ к успешному онлайн-позиционированию вашего бизнеса, гарантируя грамотный маркетинг и надежное присутствие в сети.
- Шелкограф.рф - Ваш ключ к успеху: выбор между покупкой и арендой доменного имени для бизнеса
- Оптимизируйте онлайн присутствие вашего бизнеса с шелкограф.рф, предлагающим выбор между покупкой или арендой профессиональных доменных имен для роста и узнаваемости вашего бренда.
- Доменное имя электролит.рф: выбор для электронных предпринимателей – покупка или аренда – ключ к успеху в бизнесе онлайн
- Доменное имя электролит.рф: оптимальный выбор для электронных предпринимателей, решающий вопросы покупки или аренды домена, открою новые горизонты успешности вашего бизнеса в интернете.
- Ваш успешный бизнес на эксель.рф: выгодное доменное имя для российской аудитории
- Получите преимущества краткого и легко запоминающегося домена эксель.рф, повышающего доверие российской аудитории, идеально подходя для вашего сайта и бизнеса, связанных с аналитикой и управлением данными, а также подчеркивающего уникальность и профессион
- Шикарные.рф – Открой новые горизонты бизнеса с уникальным российским доменом
- Оптимизируйте присутствие вашего бизнеса в Интернете с привлекательным доменом Шикарные.рф, обеспечивая уникальность, запоминаемость и больше клиентов через SEO-эффективную зонтичную марку.
- Шелкопряд.рф: Увеличиваем онлайн-присутствие бизнеса с выгодным доменным именем
- Шелкопряд.рф предлагает выгодные условия по приобретению или аренде уникальных доменных имен для укрепления онлайн-присутствия вашего бизнеса и привлечения целевой аудитории.
- Частное.рф: Уникальная возможность для вашего бизнеса - купить или арендовать доменное имя
- Узнайте, как приобретение или аренда частное.рф доменного имени обеспечит вашему сайту уникальность, безопасность и лояльность российской аудитории, что ведет к повышению доверия и онлайн-присутствия.
- Почему стоит купить или арендовать доменное имя целуй.рф: преимущества и рекомендации
- Погрузитесь в мир качественного контента с доменным именем целуй.рф — идеальным выбором для бизнеса и инноваций, гарантирующим узнаваемость, надежность и адаптивность вашего онлайн-присутствия на просторах интернета.
- Как купить или арендовать доменное имя чуб.рф для гарантированной прибыли и уникальных преимуществ в бизнесе | Подробный гид
- Овладейте стратегией успеха в Интернете: научитесь выбирать и приобретать доменные имена на чуб.рф для стабильного заработка и получения уникальных профессиональных преимуществ.
- Циркули.рф: Оптимальные решения для развивающегося циркового бизнеса - покупка или аренда доменного имени
- Циркули.рф - специализированный сервис для решения нужд циркового бизнеса, предлагающий купить или арендовать уникальные доменные имена, чтобы подчеркнуть уникальность и профессионализм вашего цирка.
- Доменное имя цигарка.рф: ключ к успеху в табачном бизнесе | Современная табачная индустрия
- Доменное имя цигарка.рф - это оптимальный маркетинговый инструмент для специализированного табачного бизнеса, гарантирующий быстрый рост аудитории и доверия клиентов.
- Доменное имя чистейший.рф: Неуязвимый гид для вашего успешного бизнеса
- Доменное имя чистейший.рф — это важный маркетинговый инструмент, который гарантирует высокий уровень доверия клиентов и улучшает позиционирование в поисковых системах, делая ваш бизнес более привлекательным и успешным.
- Эффективное доменное имя для чебуречного бизнеса: чебуречные.рф
- Откройте новые горизонты для развития своего бизнеса в сфере чебуреков с оптимизированным доменным именем «чебуречные.рф» и привлекайте новых клиентов, пользуясь всеми преимуществами сети Интернет!
- Купля или Аренда Домена чайнатаун.рф: Безупречные Преимущества и Перспективы Развития Вашего Бизнеса
- Аренда или покупка домена цирковые.рф: Как усилить присутствие вашего бизнеса в сети
- Изучайте, стоит ли инвестировать в приобретение или аренду домена цирковые.рф для повышения видимости и эффективности вашего циркового бизнеса в интернете.
- Доменное имя цинга.рф: ключ к успеху в онлайн-мире и стратегическое преимущество для бизнеса
- Откройте новые горизонты для онлайн-серфинга и бизнеса с доменным именем цинга.рф – идеальным выбором для укрепления вашей онлайн-представительности на российском рынке.
- Доменное имя цигарка.рф – идеальный выбор для развития бизнеса в табачной отрасли
- Доменное имя цигарка.рф - идеальный инструмент для продвижения бизнеса в табачной отрасли, гарантирующий узнаваемость и доверие клиентов в онлайн-пространстве.
- Доменное имя Хризантема.рф: Путь к успеху в интернете для вашего бизнеса
- Доменное имя Хризантема.рф - надёжный инструмент для продвижения бизнеса в интернете, гарантирующий запоминаемость, доверие и стабильный рост интернет-трафика к вашему проекту.
- Доменное имя Холодильное.рф: Привлекательный выбор для бизнеса и инвестиций
- Погрузитесь в мир энергоэффективных холодильных технологий с доступным вариантом аренды или покупки домена холодильное.рф, обеспечивая удобный доступ к вашему онлайн-представителю в индустрии глубокой заморозки.
- Аренда или покупка домена флибустьеры.рф: почему это важно для вашего бизнеса
- Обращайте внимание на аренду или покупку доменного имени 'флибустьеры.рф' – идеальный ход для создания уникального и запоминающегося интернет-пространства, связанного с флибустьерской тематикой и привлечения целевой аудитории с интересами к жизни и приклю
- Купить или арендовать доменное имя уничтожать.рф: преимущества и выгоды для вашего бизнеса
- Найдите ответ на вопросы о выгоде покупки или аренды домена уничтожать.рф, разумно инвестируйте в ваш онлайн-достояние – читайте наши подробные рекомендации.
- Аренда и Покупка Доменов на Хосты.рф: Ключ к Успеху Вашего Бизнеса
- Узнайте, как аренда или покупка доменных имен на хостинг-платформе Хосты.рф может повысить вашу онлайн-присутствие и обеспечить успех вашего бизнеса в интернете.
- Приобретайте или арендуйте доменное имя Холстен.рф: ключ к успеху на русскоязычном Интернете
- Обретите доменное имя Холстен.рф, ключ к успеху в сети, и завоюйте доверие и внимание Русскоязычной аудитории на Русском интернете.
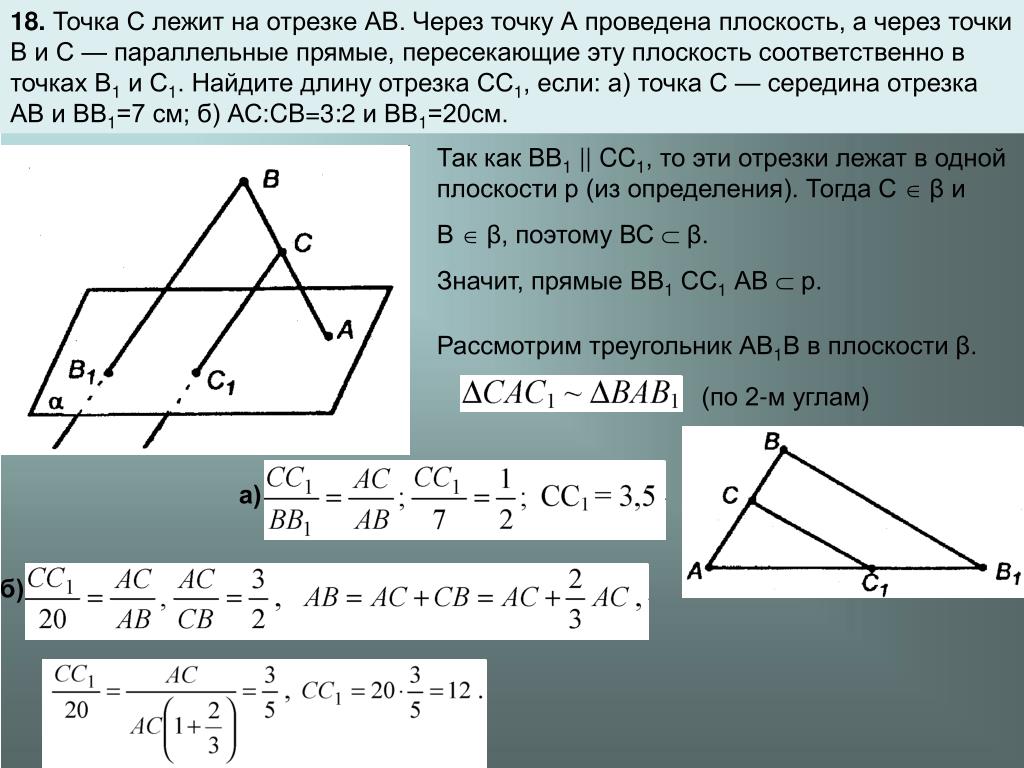
Точка расположена на отрезке, плоскость проходит через нее и параллельна двум данным прямым
Для начала, рассмотрим что такое точка с на отрезке ав. Это означает, что данная точка с лежит на отрезке, соединяющем две заданные точки а и в. Точка с находится между точками а и в и делит отрезок ав на две части в определенном отношении. Чтобы определить положение точки с на отрезке ав, мы можем использовать формулу нахождения координат точки по формуле с = (а + в)/2. Здесь а и в - координаты заданных точек, а с - координаты искомой точки с. Когда мы рассмотрим построение параллельных прямых в плоскости а через точки а и с, мы должны помнить о следующем. Для конструирования параллельной прямой, достаточно найти ее уравнение и использовать его для построения данной прямой. В данном случае мы знаем координаты точек а и с, и можем использовать эти данные для нахождения уравнения параллельной прямой. Что такое точка с на отрезке ав?Точка С на отрезке АВ играет важную роль в геометрии и математике в целом. Она позволяет решать различные задачи, связанные с расположением точек и отрезков в пространстве. Кроме того, точка С на отрезке АВ может использоваться для построения параллельных прямых в плоскости А, проходящих через точки А и С. Это свойство точки С помогает решать задачи по определению и построению параллельных линий и поверхностей.
Основные понятия и определенияПеред тем, как перейти к изучению точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с, полезно разобраться в некоторых основных понятиях.
Знание этих основных понятий и определений поможет нам лучше понять тему точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с и успешно продолжить изучение данной темы. Как найти точку с на отрезке ав?Чтобы найти точку С на отрезке АВ, нам понадобятся координаты точек А и В. Представим отрезок АВ в виде прямой, проходящей через эти две точки. Для нахождения точки С, которая будет лежать на этой прямой и параллельна другой прямой в плоскости А, используем формулу: С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) Здесь t – параметр, принадлежащий отрезку [0, 1]. Если t = 0, то точка С будет совпадать с точкой А, если t = 1 – с точкой В. Итак, мы знаем координаты точек А и В, а также значения параметра t. Подставляем все это в формулу и получаем координаты точки С. Пример:
Пусть А(2, 3) и В(6, 9). Находим значений параметра t, например, t = 0.5. С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) С(xС, yС) = (2, 3) + 0.5 * ((6, 9) - (2, 3)) С(xС, yС) = (2, 3) + 0.5 * (4, 6) С(xС, yС) = (2, 3) + (2, 3) С(xС, yС) = (4, 6) Таким образом, точка С находится на середине отрезка АВ и имеет координаты (4, 6). Существование и уникальность точки CДля того чтобы точка C существовала на отрезке AB и была параллельна прямым в плоскости, проходящим через точки A и B, необходимо выполнение определенных условий. Во-первых, для существования точки C на отрезке AB необходимо, чтобы точка A не совпадала с точкой B, иначе отрезок будет вырожденным. Во-вторых, чтобы точка C была параллельна прямым, нужно убедиться, что отрезок AB и прямые в плоскости, проходящие через точки A и B, действительно параллельны. Это означает, что угол между отрезком AB и любой из этих прямых должен быть равен 180 градусам. Если все условия выполнены, то точка C существует и является уникальной на отрезке AB, параллельна прямым в плоскости, проходящим через точки A и B. Параллельные прямые в плоскости а
Если две прямые параллельны, то их наклоны равны. Наклон прямой определяется через разность координат точек, через которые проходит прямая. Например, если прямая проходит через точки (х1, у1) и (х2, у2), то наклон прямой равен: м = (у2 - у1) / (х2 - х1). Если наклоны двух прямых равны, то они параллельны. И наоборот, если две прямые параллельны, то их наклоны равны. Кроме определения параллельности через наклоны прямых, можно использовать еще один способ - построение плоскости а. Для этого необходимо провести прямую через две точки a и с, а затем, провести скрещивающую прямую через точку a, параллельную прямой о. Если эти две прямые не пересекаются, то прямая о и параллельна прямой в плоскости а.
Уравнения прямых о и а имеют одинаковую функцию (2х), поэтому их наклоны равны и они параллельны. Как найти параллельные прямые через точки а и с?Для того чтобы найти параллельные прямые, проходящие через заданные точки A и C на плоскости, необходимо выполнить следующие шаги: Шаг 1: Определите координаты точек A и C. Для этого вам понадобятся значения x и y для каждой из точек. Шаг 2: Определите уравнение прямой, проходящей через точку A. Для этого можно использовать формулу наклона прямой, которая выглядит следующим образом: y - y1 = m(x - x1), где m - наклон прямой, а (x1, y1) - координаты точки A. Шаг 3: Используя полученное уравнение, подставьте координаты точки C и решите полученное уравнение относительно переменной m. Таким образом, вы сможете определить наклон параллельной прямой. Шаг 4: Найдите уравнение параллельной прямой, проходящей через точку C, используя найденный наклон m и координаты точки C. Вы можете использовать формулу y - y1 = m(x - x1), где (x1, y1) - координаты точки C. Шаг 5: Проверьте полученное уравнение, подставив в него координаты точек A и C. Если оба значения равны, значит, прямая, построенная по уравнению, параллельна прямой, проходящей через заданные точки A и C. Таким образом, следуя этим шагам, вы сможете найти параллельные прямые, проходящие через заданные точки A и C на плоскости. Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ. Точка с на отрезке ав и параллельные прямые в плоскости а через точки а и с Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ.
|

 Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.
Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.